Apparently there has been considerable interest in this mining situation, so allow me to elaborate on the unfinished problem along with Psycho's contribution.
First, let me apologize for my tardiness in the reply. I had to apologize to Acro first, and she demanded a weekend-long foot massage from me. Hopefully we're on good terms now, so I can continue with the mining matter at hand.
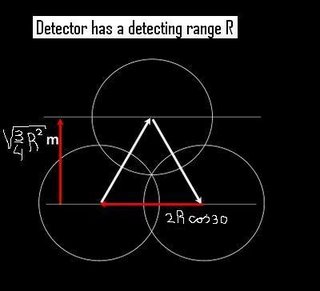
By using the example given, in simple-to-use 50 meter terms, the whole mystery is unlocked by creating some triangles within key functional areas and recruiting that fine man Pythagoreas to get to work. the key areas are as follows -- remembering that in this example, 50 meters is the standard.
While this may look odd, weird, cumbersome, and the opposite of entertaining, all this really boils down to is a long explanation that becomes a simple set of measurements. While Psycho utilized cosines and so forth, the real beauty of this grid exists in the component triangles being made up of 30, 60 and 90-degree angles. The ratios for the respective sides were again nicely assessed by Pythagoreas, with one side being half the hypotenuse, and the other side being the length of the shortest side times the square root of 3. After a few manipulations, we come up with the measurements necessary to solve the question of how far N and how far E. Psycho, you may check my work:
Now that there are numbers for this situation, the application is actually quite simple (as seen below). For any area being searched (assuming the first bomb/probe is empty), the next one should be 75 meters north and 43.3 meters east (assuming that things start in the southwest corner of the area), with the third drop being 75 meters south (the same latitude as the first) and a further 43.3 meters to the east. Once that is done, the process is repeated over and over and over for as long as you care to go. And of course, this pattern repeats in a north/south way with good regularity.
Now, when applying this to your own personal range, the measurements will come out slightly different unless your range just happens to be precisely 50 meters. In my case it is about 55 meters, while Beni's range is probably beyond man's understanding. But for whatever the personal range may be, there are simple ways to input that figure into an equation and get a sweet result that's easy to work with. Psycho has provided one means to do it, and below I am providing another way to quickly gather those numbers.
If my calculations are correct (Psycho...), this will provide a convenient way to at least map out a area or suspect patch of territory. And yes, VinzZ is right in saying that multiple bombs/probes on an empty spot will all fail -- so keep an eye out for someone mapping out a territory you are trying to map as well. A nice comfy spot far away from civilization and other miners will do nicely.
In a subsequent article I will do a little expanding on questions about the necessity of overlap and on how to incorporate finds into a territory map. this is something that VinzZ knows about as well, so ask him if I haven't blogged it (great minds think alike). Until then, bombs away!!!
Curly Twist Bender
Wednesday, November 29, 2006
My "Twist" on Mining -- Pt. 2
Posted by James Pressler at 4:14 pm 1 comments
Tuesday, November 28, 2006
Friday, November 24, 2006
My "Twist" on Mining
Hello soc! It's me again, here to share some thoughts on the optimum way to mine. While this may be more into Beni's territory, I felt the urge to put forth my 2 pecs of research and experience in an effort to start an enjoyable and educational debate. And on that note...
I do my best thinking in the shower, and that's where I was when the idea of better mining strategy came to me. I very quickly washed up, dried off, thanked Acro for showering with me, and went to the drawing board to write up some general details. Here's what I am putting together.
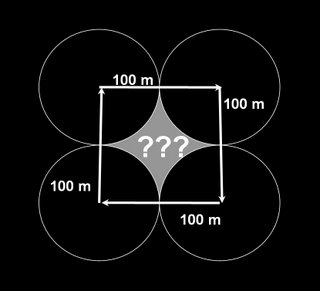
First, the standard way of mining is to try a spot out, and if it fails, march 100 meters in some cardinal direction -- N, S, E or W -- and try again. This practice creates a grid of sites that are examined with very little overlap. With the range of basic mining equipment stertching out to just over 50 meters, this seems to work out effectively -- but it neglects a key area of potential goods -- and globals!
Now, using the basic assumption of a 50 meter detection radius for mining (to keep the math easy), the 100 meter grid method does cover the north-south and east-west axes very well. However, as the pics below suggest, there is a grey area in the middle that get neglected! Now, some of that space is accounted for when using the actual detection radius of 55 meters or so, but to cover the full grid space, the detection radius would need to be 70.7 meters! And using the grid method with a 71 meter range would create a lot of overlap -- wasteful overlap at that!

 Please pardon all the upcoming math -- I do statistics, optimization and research in the boring real world -- and try to appreciate (or dispute) the results. To check out the most area with the least overlap and no neglected spots, the grid method is not the most efficient, and could end up costing extra probes/bombs when mapping out a grid. So, unless you are like Beni and made of PEDs, a little extra efficiency might help. This would be accomplished through a triangular grid system, with some awkward numbers used to determine starting points, how many meters should be marked off, and so forth. In a world of perfect mapping, it would look kind of like the following:
Please pardon all the upcoming math -- I do statistics, optimization and research in the boring real world -- and try to appreciate (or dispute) the results. To check out the most area with the least overlap and no neglected spots, the grid method is not the most efficient, and could end up costing extra probes/bombs when mapping out a grid. So, unless you are like Beni and made of PEDs, a little extra efficiency might help. This would be accomplished through a triangular grid system, with some awkward numbers used to determine starting points, how many meters should be marked off, and so forth. In a world of perfect mapping, it would look kind of like the following: Now, the more precision measurements will be displayed using an assumption of a 50 meter detection range -- with a final conversion equation to allow real ranges to be plugged in and used for real virtual world situations. The key to this is provided courtesy of Pythagoreas -- one of many fine European folks -- who did a lot of geometry, created a bunch of theorems, and founded the classes that I took at University. But in short, the sum of his work created the basic triangular formation below, and established the necessary stuff to figure out the distances given our 50 meter radius assumption (let's see a snablesnot do that!). The result should be the distance required that one has to go N or S, and the distance E or W, to create the perfect (or optimal) grid.
Now, the more precision measurements will be displayed using an assumption of a 50 meter detection range -- with a final conversion equation to allow real ranges to be plugged in and used for real virtual world situations. The key to this is provided courtesy of Pythagoreas -- one of many fine European folks -- who did a lot of geometry, created a bunch of theorems, and founded the classes that I took at University. But in short, the sum of his work created the basic triangular formation below, and established the necessary stuff to figure out the distances given our 50 meter radius assumption (let's see a snablesnot do that!). The result should be the distance required that one has to go N or S, and the distance E or W, to create the perfect (or optimal) grid.
This is a fun, if tricky bit of math and geometry. My next blog this weekend with reveal the wonderful answer, and how it can be applied to the virtual universe. If anyone has any comments, complaints or criticisms, please let me know. And if you can't find me, I'll be back in the shower...and has anyone seen Acro?
Curly "Twist" Bender
Posted by James Pressler at 7:19 pm 4 comments
Tuesday, November 14, 2006
The Calypso Post
I came across this Entropia online magazine, maybe interesting for you all.
http://www.euforces.com/CRT/calypsopost.pdf
Posted by Vince VinzZ Zyon at 9:05 am 2 comments
Monday, November 13, 2006
Go Sweat and Global
Something happened last night that i have been waiting so long for. My first Global. It was so unexpected because I was not hunting but sweating.
I have never liked sweating but not haveing much spare cash I cant deposit much at the moment so with Acronoid as my teacher and guide we set of in search of Snables. And shortly after some hunters blasted their way through our sweating party complaining about bad loot I struck it big 88Ped from a Snablesnot male Young. I only killed it because it was dry.
I was so excited yes!! I finally got my Global!!
Acronoid thankyou very much for all the tips on sweating and for taking me to Camp Caravan.
your time will come.
Posted by Teshik at 5:43 pm 2 comments